无向图的缩点与强连通分量

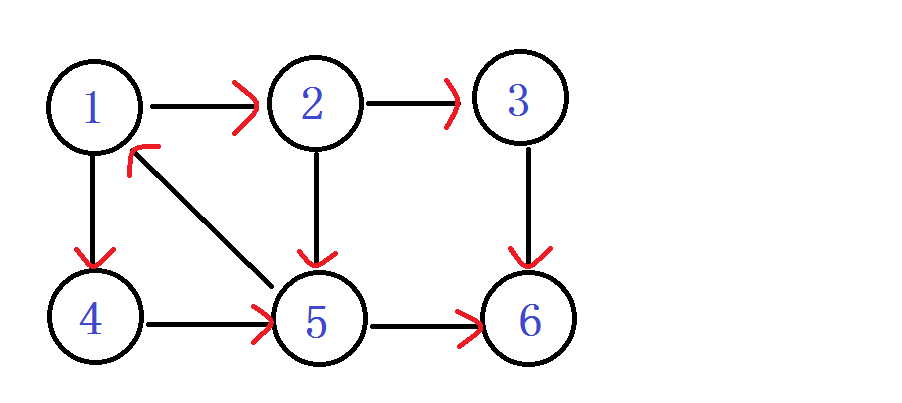
首先聊一下强连通这个概念，强连通图代表图中任意两个点可以互达，而强连通分量，则是无向图中任意强连通的子图。接下来来看这样一个图。

我们从1出发，可以很容易看到这个图中一共有3个强连通分量，分别是{1，2，3，4}、{6}、{5}。

struct node {
    int v,next;
}edge[1001];
int DFN[1001],LOW[1001];
int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y)
{
    edge[++cnt].next=heads[x];
    edge[cnt].v = y;
    heads[x]=cnt;
    return ;    
}
void tarjan(int x)//代表第几个点在处理。递归的是点。
{
   DFN[x]=LOW[x]=++tot;// 新进点的初始化。
   stack[++index]=x;//进站
   visit[x]=1;//表示在栈里
   for(int i=heads[x];i!=-1;i=edge[i].next)
   {
       if(!DFN[edge[i].v]) {//如果没访问过
          tarjan(edge[i].v);//往下进行延伸，开始递归
          LOW[x]=min(LOW[x],LOW[edge[i].v]);
    }
        else if(visit[edge[i].v ]){  //如果访问过，并且还在栈里。
          LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
      }
  }
   if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
    {
        do{
           printf("%d ",stack[index]);
           visit[stack[index]]=0;
	         index--;
       }while(x!=stack[index+1]);//出栈，并且输出。
       printf("\n");
    }
   return ;
}

步骤详情可以参考这两篇里的内容，应该可以很容易对照这个步骤。

UESTCACM 每周算法讲堂第25期 Tarjan求强连通分量_哔哩哔哩_bilibili

2016年12月1日12:22:15 本周的每周算法讲堂，视频的形式，希望大家能够喜欢。讲师:qscqesze 相关微信:UESTCACM他的weibo：qscqesze

https://www.bilibili.com/video/BV1Ls411s7dq?from=search&seid=15869929839705886798&spm_id_from=333.337.0.0

全网最!详!细!Tarjan算法讲解。_AC_Dreameng-CSDN博客

Tarjan算法讲解的博客网上找到三篇比较好的,现在都转载了,个人只研究了第一篇,正如博主所说,讲的标比较详细,清晰,剩下两篇也可以看一下. 卿学姐视频讲解 https://www.bilibili.com/video/av7330663/ 全网最详细tarjan算法讲解，我不敢说别的。反正其他tarjan算法讲解，我看了半天才看懂。我写的这个，读完一遍，发现原来tarjan这么简单！ ...

https://blog.csdn.net/hurmishine/article/details/75248876